Roche limit | Cosmicle

on

Earth's roche limit 

What is the Roche limit?

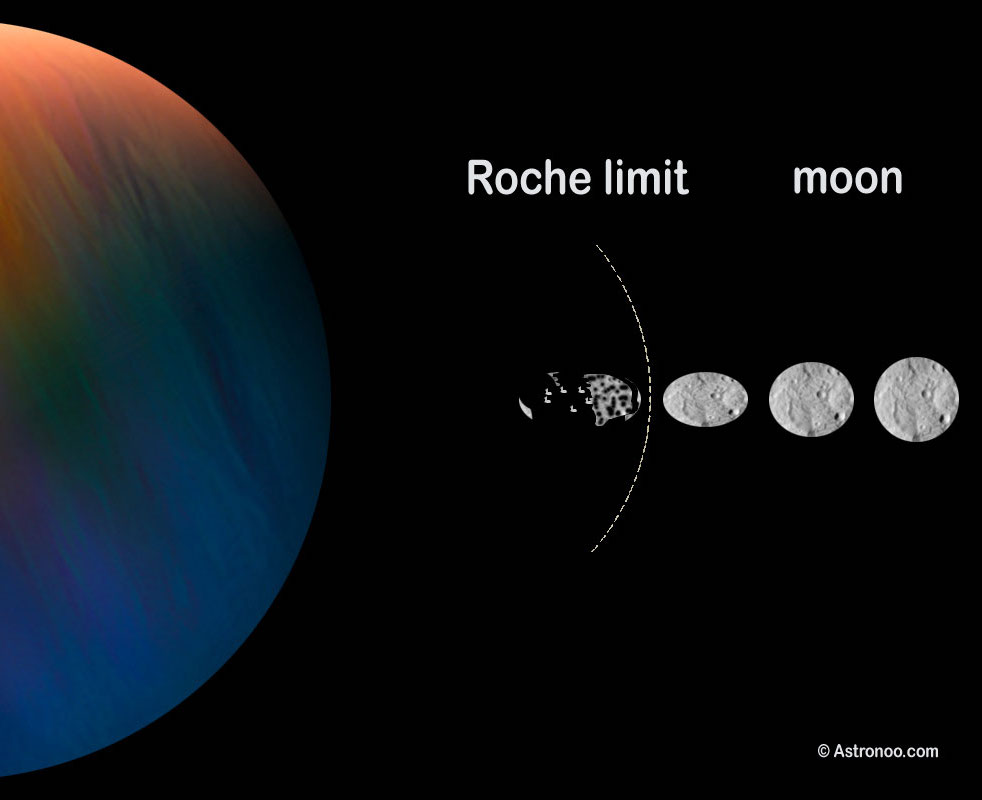
The Roche limit also referred to as the Roche radius, is the distance within which a celestial body, held together only by its own force of gravity will disintegrate due to a second celestial body's tidal forces exceeding the first body's gravitational self-attraction.

Inside the Roche limit, orbiting material will tend to disperse and form planetary rings, while outside the limit, the material will tend to combine and form solid satellites.

Saturn's Rings and The Roche Limit

The term is named after Édouard Roche, the French astronomer who first calculated this theoretical limit in 1848.

Typically, the Roche limit applies to a satellite disintegrating due to tidal forces induced by its primary, the body about which it orbits. Some real satellites, both natural and artificial, can orbit within their Roche limits because they are held together by forces other than gravitation.

Formation of planetary rings

Tidal Forces and the Roche Limit


How to calculate Roche limit?

The Roche limit depends on the rigidity of the satellite. The Roche limit refers to a body held together solely by the gravitational forces which cause otherwise unconnected particles to coalesce, thus forming the body in question.

The rigid-body Roche limit for a spherical satellite, i.e the body is assumed to maintain its spheerical shape while being held together only by its own gravity. These unrealistic assumptions simply the Roche limit calculation greatly.

The roche limit (d) for a rigid spherical satellite orbiting a spherical primary can be calculated using the Roche limit equation which is:  

d = R\left( 2\;\frac {\rho_M} {\rho_m} \right)^{\frac{1}{3}}

where R is the radius of the primary, ρM is the density of the primary and  ρm is the density of the satellite.

Notice that if the satellite is more than twice as dense as the primary then the Roche limit will be inside the primary and hence not relevant.

More accurate formula - 

d \approx 2.423 R\left( \frac {\rho_M} {\rho_m} \right)^{1/3} \left( \frac{(1+\frac{m}{3M})+\frac{c}{3R}(1+\frac{m}{M})}{1-c/R} \right)^{1/3}

This formula calculates the limit more accurately because it takes the deformation of the satellite into account. Historically, Roche himself derived the equation.


Other sources


  • https://www.cs.mcgill.ca/~rwest/wikispeedia/wpcd/wp/r/Roche_limit.htm
  • https://en.wikipedia.org/wiki/Roche_limit

Comments

Post a Comment